Author: Christian Peterson
Institution: University of North Dakota
ABSTRACT
Quantum and atomic physics can often be an abstract and difficult subject for students to learn. Derived here is a simple model for helium and two-electron systems that may make some concepts, such as screening, easier for students to understand. We extend Bohr’s derivation, assuming a natural electron configuration, to explain some of the spectral lines of helium (He). We assume that the two electrons are at 180° apart in a circular orbit due to their mutual repulsion. The spectral lines calculated, namely the specific wavelengths of light emitted by elements when they are energized, correspond to an assumed possible scenario where the two electrons make orbital transitions in unison. In this model we calculate an energy prediction for the unionized helium atom. We then predict the first and second ionization energies. Error between experimental and predicted ionization energies is about five percent, indicating that our model is reasonably accurate within the aforementioned parameters.
INTRODUCTION
In 1913, Niels Bohr introduced the Nobel Prize-winning quantized version of the Rutherford-Bohr model of hydrogen. The Bohr model supposed that electrons orbit the nucleus in rigid orbitals or paths. As energy was added to the atom, the electrons made transitions between orbitals. Energy would be released from the atom as light, and the wavelength of that light differed depending on the orbitals involved in the electron’s quantum transition. Bohr showed that this model gave quantitatively correct results by deriving the Rydberg Formula, which gives the wavelength of light emitted from the atom, again depending on the orbital transitions made by the electron (Bohr, 1913). Though the Bohr model of the atom accurately predicts the quantum nature of single electron atoms or ions, it is of little use in explaining more complex multi-electron atoms. Consequently the Bohr model was superseded by modern quantum mechanics where electrons in atoms are described using complicated wave functions. Here, we re-examine the helium (He) atom through the lens of the Bohr model in a way that may help students more easily understand multi-electron atoms and ions as opposed to using complex wave functions. Effects such as screening, the reduction of attraction to the nucleus via mutual repulsion, can then be simply accounted for when the electrons are considered as particles. Subsequently we explore the models use in conjunction with a scenario in which the two electrons transition between orbitals in unison to give roughly quantitative predictions.
HELIUM PLUS (He+)
For hydrogen-like ions, Bohr demonstrated that the Rydberg Formula for the wavelength of emitted light, namely
(1)
where RH is the Rydberg constant, Z is the atomic number, and λ is the wavelength of light emitted, could be explained by the energy differences between the quantized electron energies n. Since the Bohr model applies to hydrogen-like atoms, i.e., single-electron atoms, for the case of He+, Z=2 and RHZ2 = 4.38949264 x 107 m-1. We can use this equation to calculate the ionization potential of He+, the amount of energy required to remove that second electron from orbit, by combining [Eq. 1] with the equation for energy of a photon,
(2)
where h is Plank’s constant and c is the speed of light. We will use the case where n2 = ∞, with n2 being the orbital infinitely far from the nucleus and its energy being approximately equal to zero, in order to ionize the electron completely. Substituting [Eq. (1)] into [Eq. (2)] under this condition gives
(3)
If the ion is originally in its ground state, n = 1, the result is well known and agrees reasonably well, with an error of 0.02% when compared to experimental measurements (Table 3; Charlotte E. M., 1949).
ORBITAL ENERGY OF HELIUM
The purpose of this brief note is to show what happens if one assumes two electrons in neutral helium are diametrically opposite in a single circular orbit. First then, due to screening, the net centripetal force on each of the two electrons is equal to the attraction force minus the repulsive
force:
This is then equal to:
where Kc is Coulomb’s constant, e is the charge on an electron, r is the radius of the circular orbit,
the factor of two in the attraction force (
) is due to the two protons in the
nucleus, and the factor of two in the repulsion force (
) is due to the fact that the
electrons are separated by the length of two radii. This gives the electric force,
(4)
Kinetic energy then derives from the centripetal force
(5)
with m being the mass of an electron and v being its velocity. For each electron, kinetic energy may
be expressed as:
Electric force [Eq. (4)] can then be substituted for
Fc in [Eq. (5)] to give kinetic energy as:
(6)
Potential energy also results from the two attractive forces and a repulsive force, yielding:
for each electron. The net kinetic energy in the two-electron system must
then be
Total energy of the atom is the sum ofpotential and kinetic energies:
(7)
The next step is to derive the radius of the electrons’ orbit using Bohr’s angular momentum
postulate with the principle quantum number n, namely,
We solve first for v, and then substitute it into
which is the combination
of [Eq. (4)] & [Eq. (5)] to yield a quantized relation,
The radius becomes
(8)
The radius [Eq. (8)] can be substituted into total energy [Eq. (7)] to give
Alternatively, we find
(9)
as the quantized, two-electron energy, assuming the two electrons circulate together a diametrically opposite manner.
SPECTRAL EQUATION FOR HELIUM'S S ORBITALS
The following derivation is to find the wavelength λ of light emitted when two electrons make a simultaneous transition, we can use [Eq. (2)] and [Eq. (9)], along with the difference in
orbital energies,
which, when expanded, comes to the form of
and then:
(10)
The constant here has a numerical value of
in SI units. As shown in Table 1, [Eq. (10)] gives approximately 5.5% error when compared to experimental values. However, one can use the form described in [Eq. (10)] to fit a series of spectral lines that could appear in helium’s spectrum. This fit can be used to find a Rydberg-type constant as seen in [Eq.(1)] to fit the experimental data more accurately, as demonstrated in Figure 1. We can think of this fit as correcting for an adjustment to the columbic forces interacting, because the forces may slightly vary over time.
IONIZATION ENERGY OF HELIUM
In this section we derive the equations that predict the ionization energy of neutral helium to
helium plus (He+). The ground state energy from [Eq. (9)] is
We can calculate the energy required to ionize the first electron by starting with the kinetic energy of one electron [Eq. (6)]. Potential energy for one electron in the system can be given as,
The total energy is then
Radius from [Eq. (8)] is then substituted into the radius of the electron’s circular orbit to give
(11)
ANALYSIS
We use [Eq. (10)], which follows this Bohr-like model’s assumptions, to calculate a series of lines in the visible portion of helium’s emission spectrum. The series results from various two-electron simultaneous transitions to the state with principle quantum number n=5. Percent error is calculated based on the experimental lines that these could represent, shown in Table 1 (Richard & Peter, 2000). We then determine an effective constant consistent with experimental results, which may be thought of as an adjustment for the electron correlation and screening (Figure 1). Subsequently, we show the extent of agreement between experimental data with [Eq. (10)] using the modified constant as derived from Figure 1 (Table 2). The radius of helium in its ground state, i.e. the lowest attainable energy and orbit, calculated to be 30.24pm from [Eq. (8)] compared within a reasonable degree of error of two percent with the accepted experimental value of 31pm (Charlotte E. M., 1949).
RESULTS
Table 1: Spectral Series of Visible Light. [Eq. (10)] is used to calculate a series of spectral lines in the visible spectrum that ends on the orbital n1=5 with percent errors calculated respectively (Richard & Peter, 2000).
Figure 1: Experimental Constant Adjustment. The adjusted Rydberg-like constant is calculated (63849000 m-1) using the least square method and plotted graphically with experimental data (Richard & Peter, 2000).
Table 2: Modified Spectral Series in Visible light. Using the adjusted constant, the series is recalculated and compared to the experimental data again (Richard & Peter, 2000).
Table 3: Helium Ionization Energies. The predicted values of ionization energies, from
[Eq. (11)], [Eq. (3)], and [Eq. (10)] respectively, are compared to the experimental results, yielding percent errors (Charlotte E. M., 1949).
DISCUSSION
In this Bohr-like model of the atom, the two electrons in helium are assumed to be 180° from each other and making quantum transitions concurrently. Though this quasi-classical model cannot explain all of the spectral lines, it does present one possibility for a quantum transition scenario of the S orbitals, i.e. the spherical electron orbital in an atom. Another possible transition scenario is a model of excited helium where one electron is in ground state and the other is excited, in which some shielding will take effect, changing the energy emitted as the excited electron transitions to a lower state. One of the most influential factors in why the Bohr and Bohr-like models were abandoned was due to the discrepancies between experimental data and theoretical predictions. The predicted ionization energy of helium to He+ has a significant percent error when compared to measured results (Charlotte E. M., 1949). This may be due to the fact that the Bohr model does not account for the quantum spin of the electrons. Deeney and O’Leary (2012) discuss in detail how in the modern theory, electrons with aligned spins, i.e., the triplet state, have the lowest attainable energy. However, the Pauli Exclusion Principle forbids this possibility, resulting in a state of higher energy with anti-parallel electrons, which in turn would yield lower ionization energies as shown in Table 3. Although the Bohr model has since been superseded by the Schrödinger theory, it is hoped that this modified model could be of use to help students understand and conceptualize the quantum effects of screening and its interactions in multi-electron atoms and ions.
AKNOWLEDGEMENTS
The author would like to thank his mentors, Dennis Symalla and Dr. William Schwalm, for their indispensable ideas and support.
REFERENCES
Bohr, N. (1913). On the Constitution of Atoms and Molecules. Philosophical Magazine, 26, 1
Charlotte E. M. (1949). Atomic Energy Levels Vol. 1. Circular of the National Bureau of Standards
Deeney, F. A., & O'Leary, J. P. (2012). The Effects of the Pauli Exclusion Principle in Determining the Ionization Energies of the Helium atom and Helium-like Ions. European Journal of Physics, 33, 667-675
Gasiorowicz, S. (2003). Quantum Physics (3rd ed.). New York, NY: Wiley Richard, P., & Peter L. (2000). Optical Emission Lines of the Elements.
England, Wiley & Sons Ltd Zattili, N. (2009). Quantum Mechanics: concepts and applications 2nd ed. New York, NY: Wiley









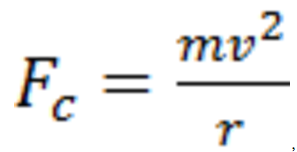


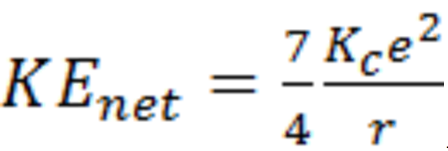



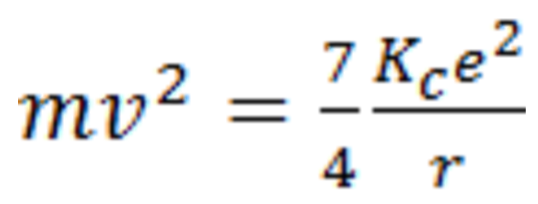








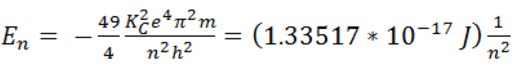
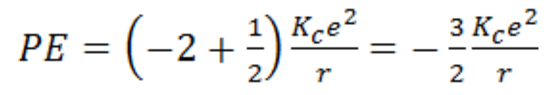


![Table 1: Spectral Series of Visible Light. [Eq. (10)] is used to calculate a series of spectral lines in the visible spectrum that ends on the orbital n1=5 with percent errors calculated respectively (Richard & Peter, 2000).](https://images.squarespace-cdn.com/content/v1/5443d7c7e4b06e8b47de9a55/1488342513486-MMAOVMRZ4KO8MAF0DD6T/image-asset.png)


![Table 3: Helium Ionization Energies. The predicted values of ionization energies, from [Eq. (11)], [Eq. (3)], and [Eq. (10)] respectively, are compared to the experimental results, yielding percent errors (Charlotte E. M., 1949).](https://images.squarespace-cdn.com/content/v1/5443d7c7e4b06e8b47de9a55/1488342538552-ZQGE7GR58EZHDS51A5FZ/image-asset.png)