Author: Brittany Raffa
Date: September 2007
"A mathematician confided
That a Moebius band is one-sided,
And you'll get quite a laugh,
If you cut one in half,
For it stays in one piece when divided"
The shape of the Moebius band is a 77 year-old mathematical riddle that has been solved by Dr. Gert van der Heijden and Dr. Eugene Starostin from the University College of London.
Courtesy of www.scientificamerican.com
The Moebius band (or strip) is a surface with only one side and one edge. It is easily constructed by taking the end of a strip of paper, twisting it through 180 degrees and taping it to the other end. The wider the paper strip, the more triangular and flat the shape, similar to what happens when paper is crumpled. The problem with the Moebius band has always been the inability to algebraically address the band, explaining the odd shape with an equation.
The mathematical phenomenon is named for the astronomer and mathematician August Moebius (1790-1860). He was a professor at the University of Leipzig in Germany who had studied theoretical astronomy with Carl Gauss, another German nicknamed the "prince of mathematicians". Rewinding to 1858, the mathematical world inside the Paris Academy was locked in tension because no one could provide a geometrical theory for the polyhedra. The academy offered a prize for a mathematical description of the polyhedra and it became Moebius to solve the problem and subsequently publish his notebooks containing the solution in 1865. The notebooks revealed, among other concepts, that of the Moebius band.
Courtesy of www.abc.net
However, August Moebius was not the first to discover the Moebius band. The younger German mathematician, Johann Listing (1808-1882), published his discovery in 1861, four years earlier than Moebius'. It is not quite sure why his name was never given to the peculiarly shaped object and why we are not currently discussing the Listing band.
Drs. Van der Heijden and Starostin describe the complication in a letter written to Nature Materials and published online July 15 of this year: Finding its characteristic developable shape has been an open problem ever since its first formulation. It is in the same letter that they explain the solution. The August 2007 issue of Nature Material illustrates how Drs. van der Heijden and Starostin devised a set of differential equations to calculate the precise shape of the band and to define the maximum width for a band in relation to its length.
To calculate the shape one must know the aspect ratio (ratio of width to length) and the elastic properties of the material from which the band is made. Areas of different energy density determine the shape. Energy density is the stored elastic energy within the strip due to bending. The image below categorizes the energy density according to color: red areas contain high energy density because the band is heavily bent, whereas blue areas have the least density due to their flat shape and the lack of tension caused by bending.
The discovery of the Moebius shape is opening doors to abounding applications. Scientists now possess a key to open multiple doors and subsequently analyze the structural properties of macromolecules and crystals grown in the shape of the Mobius band as well as model the structure of new drugs.
Courtesy of www.sciencenews.org
Although there is a vast terrain of applications still to be covered, much has already been achieved by utilizing the band's shape. In 1923 Lee De Forest obtained a U.S. patent for a filmstrip that records sounds along the entire length of the Moebius-shaped strip, and the idea was followed by tape recorders with a twisted tape in order to run twice as long. Conveyer belts in the form of a Moebius band were started to be used in 1979 with the patent by B.P. Goodrich Company. These enormous Moebius bands last twice as long as conventional belts because an equal amount of wear is applied over the entire surface area of the belt.
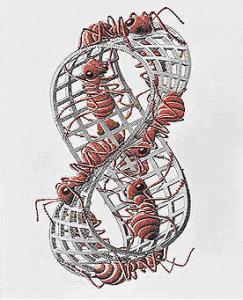
Fascination for the peculiarities of the looped object has also inspired many artists. Dutch artist M.C. Escher's painting Moebius Strip II depicts ants that never cross an edge as they crawl the band's surface. Even Stargate has explored the subject with an episode entitled "Moebius" that deals with time travel where alternate timelines wrap around a Moebius band. Nelly Furtado's song "Hey, Man!" includes these lyrics:
"We are a part of a circle
It's like a Mobius strip
And it goes round and round
Until it loses a link"
It is decisive for its abnormality that the Moebius band has gained such vast interest in an array of sectors. The breakthrough by the two English scientists of defining the shape of this object that hangs covered with ants on the walls of the National Gallery of Canada has thus dropped the first chip in a domino effect that will spur further ideas and technology.
Cool tricks: After making the band, take scissors and cut it in half lengthwise along the entire band. Rather than having two separate bands, you'll have one with twice the length and another twist, no longer a Moebius band. Cut the band you now have in half lengthwise. You'll get two interlocking rings. Magicians used this trick.
Reviewer - Antje Heidenmann, Pooja Ghatalia
Publisher- Konrad Sawicki