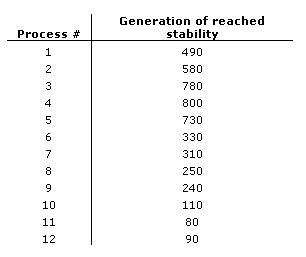Authors: Evan Hourigan and David Eck
Abstract
In this paper, the genetic algorithm is used to investigate the evolution of cooperation based upon automata that play in an iterated prisoner’s dilemma tournament. Cooperation evolved from a state of randomness. Furthermore, it is shown that “niceness”, as defined by Robert Axelrod, is unstable in this model, and, contrary to previous speculation, selective pressure is needed to stabilize niceness. A multiprocessing approach also shows that cooperation can spread through migration among multiple evolving populations.
Introduction
Can cooperation evolve in a society of egoists without the existence of a central authority? This an intriguing question because, in nature, we find that evolution rewards the efforts of individuals with selfish motives. With a limited supply of life-sustaining resources available to a population, an organism must compete with others in its population to obtain resources essential to its survival and maximization of reproductive success. Since it is the selfish behavior of the organism that ensures its self-preservation, there is no reason for cooperation to take place. On the other hand, we know that cooperation does indeed take place—ants work together in construction and the gathering of food for the benefit of the colony; people cooperate with one another on a day-to-day basis.
Figure 1 . Payoff matrix for the prisoner’s dilemma game.
This question—the problem of cooperation—has been investigated in the work of Robert Axelrod (1984). In his work, Axelrod uses a model known as the prisoner’s dilemma game to studying cooperation. Two players take part in the prisoner’s dilemma game. Each player must make a move, either to cooperate or to defect with the opposing player, without knowing what the other player will do. Scoring is calculated as shown in the payoff matrix (Figure 1). It is known by both players that acting selfishly—defecting—yields a higher payoff than cooperating no matter what the other player does, and so the natural decision is to defect. However, it is also known that by cooperating, both players can collectively do better than if both defect, hence the dilemma. Axelrod proposes that for cooperation to take place, a series of games must be played so that players can anticipate future interactions, and base their move decisions upon previous game outcomes. In this model, the iterated prisoner’s dilemma, it becomes rational to cooperate.
To satisfy his interest, namely which strategies were the most effective in the iterated prisoners dilemma game, Axelrod had participants from various disciplines submit hand-crafted computer programs. Each program defined a strategy for playing the game with another program. In a round-robin style tournament, he matched each program submitted with all other programs, and ranked them based upon their scores. In each tournament, the simplest strategy, TIT FOR TAT (in which the first move is to cooperate, and then in each subsequent move to copy the opposing player’s previous move), received the highest scores. Given its success, Axelrod questioned the robustness of the strategy—he wanted to see how well it would do in other environments. Knowing that the success of any particular strategy depends upon the environment with which it interacts, Axelrod devised a set of pseudo-evolutionary experiments in which the frequency of each strategy in a population of strategies was dependent on its success in preceding tournaments. This variation on survival of the fittest is not to be confused with a true evolutionary experiment, since the set-up of the tournaments does not allow for new behavior to emerge. In contrast, it simply allows those more successful to become more frequent.
In this ecological simulation, Axelrod found that those strategies demonstrating a particular behavior known as niceness ultimately dominate a population initially filled with equal proportions of both nice and non-nice strategies. To clarify: A strategy is defined to be nice if in its interaction with any other strategy, it is never the first to defect.
This study extends Axelrod’s research to an evolutionary simulation. Instead of starting with a population composed of hand-crafted strategies, and then multiplying its frequency in subsequent generations, this study uses the genetic algorithm to explore another hypothesis. This new hypothesis is that cooperation can emerge from an initially random state by using the genetic algorithm to evolve generations of individuals (represented as computational devices such as automata) capable of playing the iterated prisoner’s dilemma game. Furthermore, this study examines how strategies that exhibit niceness perform in an evolutionary simulation.
Methods
In Axelrod’s work, he uses hand-crafted programs to play the prisoner’s dilemma game. With the genetic algorithm, however, it would like to be discerned whether or not cooperation can emerge from a state of randomness. Therefore, each individual must begin with randomly composed genetic data that defines a strategy for playing the iterated prisoners dilemma game with other individuals in the population. The genetic algorithm will evolve new generations of individuals with chances of reproduction based upon an individual’s fitness score (where fitness in this case is determined by how well the individual plays the iterated prisoner’s dilemma game against other members of the population.) In the genetic algorithm, individuals in the subsequent generation are created by applying two genetic operators: recombination and mutation. The new individual’s genetic data is defined by recombining the data of their selected parents. Depending upon probability, the genetic data of the new individual may also undergo a small mutation. An in-depth discussion of the genetic algorithm can be found by consulting Goldberg (1989). Furthermore, like the hand-crafted strategies Axelrod uses, individuals must be able to take into account a memory of past interactions with the opposing player when deciding whether to cooperate or defect at any given point in the game. An excellent, uncomplicated way of representing past knowledge is through the use of a state machine.
Unlike a computer, a state machine’s memory capacity is set permanently upon its creation, and cannot be changed throughout its lifetime. This type of machine is known as an automaton. Typically, automata are fed input strings, and based upon each character fed to it, the automaton changes state according to its state transition function. After the entire string has been consumed by the automaton, it is said to be in either a state in which the string is accepted, or in a non-accepting state. Formally, this type of computational device is known as a deterministic finite-state automaton (Lewis and Papadimitriou 1998). We need an automaton that takes a series of cooperate or defect moves and, instead of classifying strings, produces outputs, where the outputs are the corresponding cooperate or defect decisions for the particular strategy.
This type of automaton, one that receives inputs and changes states to produce outputs, is known as a transducer. Like an automaton, a transducer has a start state. When an individual meets someone for the first time to play the iterated prisoners dilemma game, both individuals are in this state. In the first game, each player makes the move defined in the start state. In each subsequent game, based upon the move of the opposing player in the previous game, each player transitions to a different state according to his or her genetic data and then makes the move defined for that state.
Figure 2. Sample genetic data array and state diagram for a five-state automaton capable of playing the iterated prisoner’s dilemma.
To represent the genetic data for an individual, two arrays (indexed by state, where the length of the arrays is the number of states) are used. A two-dimensional input array T[s][m] represents the transition function; that is, if s is the individual’s current state, and m is the move of the opposing player, then T[s][m] is the next transition state. The one-dimensional output array represents the corresponding move of the individual for any particular state. As an example, a genetic data array and its corresponding state-transition diagram for a five-state automaton capable of playing the iterated prisoner’s dilemma game is shown in Figure 2.
With the automaton model as an appropriate representation of an individual in a genetic algorithm population, the program necessary to carry out this particular implementation of the genetic algorithm was coded in C++. In this program, the individuals that participate in the evolution have twenty states and begin with randomly filled genetic data. A population of 100 such individuals is evolved using the genetic algorithm. In each generation, each individual plays every individual in the population for 100 games. The cumulative score achieved by playing all other individuals in the population determines the probability that an individual will be selected for reproduction when the next generation is created. When an individual reproduces to create offspring for the next generation, his or her data can be crossed over with another selected individual, and may also undergo a mutation. Furthermore, to test Axelrod’s prediction that niceness will proliferate in a mixed population, a test was developed to determines whether an individual is nice or not by tracing through his or her state data, testing his or her responsiveness to cooperate moves, and making sure he or she is never the first to defect.
Single Processor Implementation Results
Figure 3. Cooperate-cooperate move averages, by generation, for 100 trials.
To investigate the first hypothesis, namely that cooperation can evolve, the program kept track of the total number of cooperate-cooperate moves in each generation for 1000 generations (i.e, the number of times any two individuals in the population cooperate with one another for a single prisoner’s dilemma game in each generation.) It then averaged together these totals, by generation, over 100 trials. Results are shown in Figure 3.
Recall that since in each generation, 100 individuals are each matched against 99 other individuals to play 100 games with each other, the maximum possible total of cooperate-cooperate moves per generation is 495,000. We see that in Figure 3, cooperate-cooperate moves reach a plateau height of 450,000, coming very close to the maximum possible value. This shows that cooperation indeed tends to increase. An interesting feature to note, however, is the initial dip that occurs between generations 0 and 50 preceding the upward trend. This may be because when the population is first created, the strategy of cooperative individuals has not had a chance to develop. Therefore, defectors have an advantage and higher fitness scores that allow them to proliferate. Accordingly, in subsequent generations, the population would become increasingly dominated by defectors. However, since they cannot thrive off one another, their fitness scores would dramatically decrease. After this nadir, cooperators with a smarter game playing strategy may begin to emerge. If these cooperators are able to respond to defectors by defecting, while at the same time cooperating with others, then their success will allow them to dominate in subsequent populations. This would account for the upward trend following the initial dip in Figure 3.
Figure 4. Percentage of nice individuals by generation, for 5000 generations.
With these results, we might consider how the degree of niceness manifested by individuals in a population would affect our results. Having developed a measure of niceness, Axelrod’s prediction that niceness will proliferate in a mixed population was tested. For this, the program was set to run a single trial of 5,000 generations. In every generation, the percentage of individuals that pass the niceness test is calculated and reported. Results are shown in Figure 4.
From Figure 4, it is clear that niceness prefers either a low or high percentage range, as it periodically fluctuates between the two ranges. Evidently, percentages close to either 0% (none) or 100% (all) have a certain degree of stability. Niceness alone, on the other hand, is very unstable over time—that is, it does not reach a certain point and remain there indefinitely. This effect more than likely has to do with the fact that in the calculation of fitness, there is nothing that truly gives selective advantage to nice individuals. We can distinguish between two types of niceness—niceness exhibited by either smart or dumb cooperators. When defectors are present, smart cooperators retaliate immediately to uncalled-for defection. On the other hand, dumb cooperators do not exhibit this degree of skill, and by not retaliating to defection, are easily taken advantage of. In a population of cooperators, smart cooperators have no advantage over dumb cooperators. Since each individual has a capacity for multiple “gene” combinations, and is essentially unique, some individuals may be smarter than others.
To explore how trends in niceness are affected by and individual’s degree of skill in making cooperative game decisions, an “IQ test” was developed. This IQ test simulates repeated interactions with an individual in which a certain number of cooperate moves is followed by a defect move. The IQ score is computed by awarding points to an individual when he or she responds to a defection by defecting in turn. The program was changed so that it recorded for each generation, over a course of 4,000 generations, the percentage of nice individuals in the population and their average IQ scores. Results are shown in Figure 5.
Figure 5. Niceness % and Average IQ for 4000 generations without malignment.
As Figure 5 shows, an interesting effect can be observed with IQ data for the span of generations in which niceness remains at a peak of about 100%. During certain segments of this generation span (i.e., generations 100-200), IQ maintains a very close relationship to percent niceness. Whereas in other segments (i.e., generations 2500-2600), IQ does not seem to bear relationship to percent niceness. The former portions of the graph may be representative of a population of smart cooperators, that is, individuals that are smart about being nice. In contrast, the latter portions of the graph are representative of a population of dumb cooperators. We see here that during a time when the proportion of nice individuals remains near 100%, there can be a “genetic drift” in the IQ.
Figure 6. Niceness % and Average IQ for 4000 generations with malignment.
Recalling Axelrod’s postulation that nice individuals will ultimately dominate a mixed population, we see that niceness per se is not enough. In order to stabilize niceness in a population, some sort of selective pressure is needed to encourage nice individuals to exhibit smart behavior. A natural way of eradicating dumb cooperators from the population, while leaving smart cooperators intact, would be to constantly introduce defectors into the population to prey on dumb cooperators. This procedure, now referred to as malignment, was implemented by changing an individual’s genetic data so that he or she defects in all circumstances. For the next trial, the program was changed so that in each generation, for 4000 generations, fifteen percent of the population was maligned—that is, made into defectors. Results are shown in Figure 6.
As Figure 6 shows, about generation 1685, the population does indeed reach a state of stability. Recalling that since 15% of the population is set to be maligned each generation, 85% niceness is the highest one can expect. It can be seen from Figure 6 that in order to stabilize niceness, the right kind of selective pressure was needed. This was accomplished by adding defectors to the population each generation.
Multiprocessor Implementation Results
In the aforementioned trials, each of which were run on a single processor machine, niceness stabilization did not appear until the malignment process was added to give adequate selective pressure to smart cooperators in the population. So, typically, after a few hundred generations of a trial like those featured in Figure 6, a population would reach a state of stability. However, this was not the case in all trials. Sometimes, niceness remained at zero for the entire trial and never offered any sign of stability. This could have been due to a lack of anything remotely close to niceness in the gene pool. Even despite the randomness and change introduced by mutation and the selective pressure to have a high IQ, if the population lacked the presence of even slightly cooperative individuals, then there may have been nothing present in the gene pool from which niceness could emerge. Suppose that now in a separate, but nearby population, evolution took a different path. In this nearby population, niceness does emerge and reach a state of stability as in some of the more successful trials discussed above. If a small portion of these smart cooperators could migrate into the unsuccessful population, they might provide a basis for cooperation and niceness to emerge there.
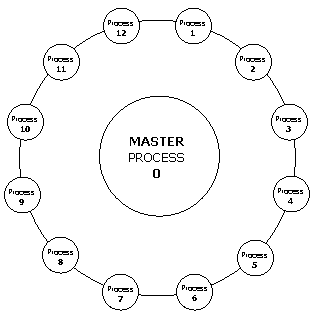
Figure 7. The circular arrangement of processes in this parallel implementation.
To test this hypothesis, a multiprocessing model of the genetic algorithm was used. Processes are communicated with each other through message passing in this algorithm. This procedure was implemented using a message passing library known as MPI (Quinn 2004). Each process ran a separate population. To simulate a migration from one population to another, the migration is encoded in a message. The parallel implementation was configured using a master-slave process model that can be visualized as shown in Figure 7.
Thirteen processes are used in the model. Twelve of the thirteen processes are slave processes, each one dedicated to evolving its own population of individuals with malignment. Each slave can engage in migrations with only two other processes—the neighboring processes on its left and right side. The thirteenth process was the master responsible for controlling the migration of each of the slave processes by sending commands to “do migration”. It was also capable of receiving and reporting statistics from each of the slave processes. Lastly, the master process ensured that each slave process evolved at a fairly consistent rate with the rest of the slaves by enforcing a checkpoint. In the checkpoint, each of the slaves evolves its own process until a specified checkpoint generation number is reached. Once the master knows that each slave process has reached that checkpoint, the command to continue is sent out to the slaves.
Table 1. Results of the parallel implementation for each of the twelve slave processes in which migration is disabled.
Since we are testing mainly whether or not having regular migrations between isolated populations has an effect on the emergence of niceness, two trials, each of 1000 generations, were run. First, a control trial was run in which migration had been disabled in order to determine how the processes in the parallel implementation will fare. This was then compared to a second trial in which migration was enabled. The results of the first trial are tabulated in Table 1. The niceness results for each of the twelve slave processes in our first trial with disabled migration was much like the results from the non-parallel implementation trials. For some of the processes, the conditions were right and niceness emerged. For other processes, niceness simply never emerged.
Table 2. Results of the parallel implementation for each of the twelve slave processes in which migration is enabled.
Results of the second trial are tabulated in Table 2. Process 11 is the first to reach a state of stability at generation 80. Shortly thereafter, neighboring processes to the left and right of process 11 reach states of stability. A chain effect takes place as stability arises consecutively in a leftward direction from processes 9 and 10, and in a rightward direction from processes 12 and 1. This stability propagates in both directions around the chain until the last process, process 4, reaches a state of stability at generation 800. Furthermore, after certain processes have reached stability, and one of their neighboring processes has not, stability is maintained despite equally frequent migrations of non-cooperative individuals from the unstable neighboring process. These results strongly support the hypothesis that niceness will spread through migration.
Discussion
Using the genetic algorithm, this study has shown that cooperation tends to increase from an initially random state in the iterated prisoner’s dilemma game. In this model, niceness was shown to be unstable when left alone—a population of nice but unskilled players can be taken advantage of by any defector through chance. By introducing selective pressure, effects of genetic drift upon IQ were minimized, and niceness was stabilized. In the multiple processor model, this study has shown that cooperation not only tends to increase, but that it also spreads through migration.
It would be interesting to see how results may changed by altering certain parameters that, for the length of this study, have remained constant. For example, what effects would be seen by increasing or decreasing the population size? Also, how would the automata perform if the number of states available with which to make decisions is either increased or decreased? Could the number of states be variable, and could they actually evolve as well? Most interesting, however, would be the results from an implementation that allows future opponents to take into account another player’s reputation from playing others. If players are able to have access to such information, can they use it to make better choices at the time they play with that person?
Source Code
This paper is based upon a senior honors thesis completed in April 2004 at Hobart College, Geneva, New York. A complete copy of the thesis, including source code for programs, is available at http://math.hws.edu/~hourigan/honors/.
References
Axelrod R. (1984). The Evolution of Cooperation. Basic Books.
Goldberg DE. (1989). Genetic Algorithms: in Search, Optimization, and Machine Learning. Addison-Wesley Publishing Company, Inc. Reading, Massachusetts.
Lewis HR and CH Papadimitriou. (1998). Elements of the Theory of Computation. 2nd ed. Prentice-Hall. Upper Saddle River.
Quinn MJ. (2004). Parallel Programming in C with MPI and OpenMP. McGraw-Hill. New York.