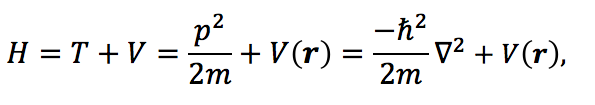Non-Hermitian Wave Mechanics: An Unorthodox Way into Embedded Systems

Author:  Felix B. A. Tellander & Karl-Fredrik Berggren
Institution:  [1] Department of Astronomy and Theoretical Physics, Lund University, SE- 223 62 Lund, Sweden [2] Department of Physics, Chemistry and Biology (IFM), Linköping University, SE-581 83 Linköping, Sweden
Date:  September 2017

doi:10.22186/jyi.33.4.87-90

Full Issue: September 2017 Special Edition

Abstract

This review outlines an unconventional but timely formulation of quantum dynamics of systems in contact with an environment. This alternative approach to traditional quantum mechanics is generic and is currently gaining attention in a number of fields as, for example, quantum scattering and transport, optical waveguides, devices embedded in an environment, oscillatory classical systems, RLC circuits and other open systems with loss and gain. Here we briefly outline this formulation in which the condition of space-time reflection (PT-symmetry) plays a central role. If PT-symmetry is broken upon parametric change, real energy levels generally turn complex. At the onset of such a symmetry breaking levels coalesce at “Exceptional Points” (EP).

Introduction

In 1926, Erwin Schrödinger formulated his famous non-relativistic equation for matter waves. In this form quantum mechanics (QM) has since then remained a never-ending success. It expands the classical Newtonian mechanics for particle orbitals into the world of quantum matter as atoms, molecules, solid matter, micro- and nano-scale devices, etc., in which particles acquire wave properties. For this reason it is also referred to, particularly in the early years of the new theory, as wave mechanics (WM) with reference to common wave phenomena present in acoustics, electromagnetism, vibrational structures as membranes and drums, hydrodynamics and more. The predictive power of QM is, as well known, overwhelming.
In short, traditional QM as above rests solidly on a number of postulates as (Schiff, 1968):

(a) A physical system is represented by a wave function Φ(r,t) which holds all information of a system;
(b) Physical observables, as for example momentum p, are represented by Hermitian operators meaning that associated eigenvalues are real numbers and equal possible outcomes of measurements;
(c) The operator representing energy, the sum of kinetic energy T and potential energy V, is the usual Hamiltonian

(1)

where m is the mass of a particle which moves under the influence of a real potential V(r) (ℏ is the reduced Planck constant h/2π). When V(r) does not depend on time t the eigenvalues En of the Hermitian Hamiltonian H are the energy levels of system.
(d) The time evolution of the wave function is given by the time-dependent Schrödinger equation

(2)

For the case above one then has

(3)

where ψn(r) is the n:th stationary solution Hψn=Enψn with real eigenvalue En.
In this review we will introduce an extension (PT-symmetry) to the well known Hermitian QM and describe its implications on QM as well as analogous classical systems. After reviewing the background and current state of the field we discuss some open problems and suggest further studies with the goal to inspire new and clever ideas. Today we lack an experimentally realized PT-symmetric QM system, but with new efforts and ideas that will surely change soon.

A new Paradigm: Non-Hermitian QM and Parity-Time (PT) Symmetry

Measurements in QM return the eigenvalues of observables; for example, a measurement of a particle’s energy yields an eigenvalue of the Hamiltonian. The important assumption of Hermitian operators guarantees that eigenvalues are real and that QM is consistent with measurements. However, more lately it has been argued that the requirement of Hermiticity may be too taxing. Can the energy levels be real also for a Hamiltonian that is complex, i.e., a non-Hermitian one? Under certain circumstances, the answer is yes. Bender and Boettcher (1998) showed how this happens when a system is symmetric under the combined PT operations of parity, or mirror symmetry, (P) and time-reversal (T). These symmetry operations translate to p→-p,r→-r for parity and p→-p,r→r,i→-i for time reversal. Enforcing this symmetry implies for the potential to satisfy V(r)=V^*(-r) and thus there is a balanced flow, i.e., gain versus loss is harmonized (Bender, 2005, 2007; Weigert, 2004). To get an understanding of the role of the complex potential V(r)= V_Re(r)+ iV_Im(r) consider the simple case of a pair of nearby even and odd states that are localized, for example, to the interior of a closed cavity (Figure 1). Let the solutions for the “unperturbed” case V_Im(r)=0 be E1 and E2. Under a parametric change such that V_Im(r)≠0 the two levels will interact according to the 2×2  matrix equation

(4)

(5)

where Vint is the interaction matrix element between the initial states 1 and 2, i.e., V_int= <1│V_Im|2>=<2│V_Im|1>; c1 and c2 are the mixing coefficients for the two states. The eigenvalues of the mixed states are

(6)

The modified eigenvalues are evidently real as long as energy gap between states 1 an 2 is larger than |2V_int|. There is a balance between gain and loss. However, as the gap becomes equal to abs(2V_int) on further parametric increase a profound change takes place. The eigenvalues coalesce into a common value referred to as an exceptional point (EP); beyond this point the eigenvalues become complex. Rewriting Eq. (6) as

(7)

The time-dependent solutions in Eq. (2) are now

(8)

Beyond the exceptional point there may thus be either exponential decay or growth of the states.  The outline above is a rather elementary one but points to the existence of EPs into which states, may coalesce on parametric change. If we consider the exponentially decaying states, which would apply to fermions because of the Pauli principle that forbids double occupancy, one should thus have the possibility of switching a state on and off by playing with V_int.

In the next section we will discuss the specific example of a quantum in contact with an environment. There will be a number states and for this reason one will have to use more refined methods than above to solve the Schrödinger equation, in this case numerical methods based on finite differences. As we will find the occurrence of EPs is a more complicated story than above, they may come and go with the gain/loss parameter V_int.

A Two-Dimensional Quantum Dot in Contact with an Environment

There is a rich variety of quantum dots fabricated from different materials for different purposes. They may be three- or two-dimensional objects embedded in solid materials, colloidal nanocrystals, etc., with intriguing physics and vast applications. A common feature is, as already the name indicates, that states are confined within a dot are quantized because of its smallness, typically in the nanometer regime. Research, basic and applied, remains very dynamic and there is a rich literature with many good monographs, see for example (Klimov 2010) and more.

Here we will focus on a particular kind of quantum dots that may be created in layered semi-conductor hetero-structures like Ga,_1-xAl_xAs/GaAs. Because of a mismatch between the band-gaps of the two materials and modulation doping with donor atoms there will be an effectively two-dimensional electron gas that resides at the interface. A smart step is to add metallic top layer/gate which makes it possible to vary the density of electrons, even to deplete it. Another smart step is to use lithography to shape the electron gas into small structures like one-dimensional wires, dots of various geometries, combinations of such objects into networks, etc., as for example described by Ferry, Goodnick, & Bird (2009).

Here we present a schematic model of a circular two-dimensional quantum dot embedded in a hetero-structure (Figure 1). The dot contains a number of electrons, usually small, that may be varied via the top gate. There are also pairs of ports that serve as emitters and collectors. In Figure 1A, for example, we may let the left port L be purely imaginary with V_L=iV_Im and V_R=-iV_Im for the other port R. Evidently there will be a current flowing through the dot. Related configurations have been elaborated for an electron/microwave billiard (Berggren et al., 2010) and, most recently, for interacting Bose-Einstein condensates (Schwartz et al., 2017).

Figure 1. Schematic picture of two-dimensional circular dots. (A) shows the case with two opposite ports with complex potentials VL(x) = VR*(-x). The interior potential is real and may be set equal to zero. The potential in the exterior region may be set to infinity, i.e., wave functions are confined to the circular area and ports. The vertical line is the line of reflection. The two ports serve as source and drain. Because of PT-symmetry, gain and loss can balance each other. (B) shows a dot with several ports with the possibility of combining the corresponding potentials according to the different symmetry lines and PT invariance. The flow of particles between the ports may thus be monitored by flexible pairings of the potentials in the different sections, i.e., the system will act a bit like a switchboard. While retaining PT-symmetry, the imaginary part of the potential may be chosen differently for the pairs giving rise to a more complex two-dimensional landscape of EPs. Obviously we may also consider more ports than just four.

As shown in Figure 2, the pair of levels may change under the parametric change, and we recover the EP discussed in the previous section. In addition we find, however, that there is another EP on further increase of the interaction, i.e., the state with real eigenvalues is restored. The calculations are more cumbersome than the analytic analysis above; a convenient approach is to turn to numerical finite difference methods described previously (Tellander & Berggren, 2017). Indeed, this method allows for a greater number of states, than just two as was discussed above. With a larger number of states one can expect more EPs to appear in the spectrum. However, the EPs only seem to appear over a finite range of VIm (Tellander & Berggren, 2017) which means that the spectrum can, as in Figure 2, be divided into three regions:the left region where V_Im is less than the critical values and all eigenvalues are real, the finite critical region where many EPs exist and the rightmost part of the spectrum where most of the eigenvalues are again real. This crossover between different dynamical regimes is called a dynamical crossover and is of great importance for experimental studies of non-Hermitian QM. In the region of many EPs, the transmission through the system should be enhanced and the states that remain complex in the right region of the spectra are believed to be associated to superradiant modes (a collection of emitters, such as atoms, that radiates strongly due to coherence) studied in atomic physics. Whether superradiance really can be viewed as a dynamical crossover is an unanswered question (Rotter and Bird, 2015). A system with more gates (Figure 1B) allows for a more direct measurement of EPs and has the possibility to settle the long-lived discussion in the field about the geometric phase obtained by a state when an EP is encircled in the parameter space. This phase is geometric in the sense that it is independent of the path that encircles the EP; compare with Cauchy’s theorem for complex curve integrals or the classical experiment using Foucault’s pendulum to prove that the earth rotates around its own axis. The system in Figure 1B can have one independent imaginary potential for each pair of leads and the parameter space is therefore two-dimensional. This system could therefore be transported around an EP and the phase change of the wave function could be extracted. Similar experiments in analogous systems such as microwave (Dembowski, 2001) and exciton-polariton (Gao, 2015) billiards have been preformed but a pure quantum experiment is still in the future.

Summary and Outlook

Above we have outlined in a schematic way how quantum states and currents in a biased PT-symmetric cavity in contact with surrounding reservoirs may be emulated by means of complex potentials for source and drain. This is, for example, of considerable computational convenience when modelling transport in real devices at small source-drain bias. This idea is already found to work well for the analogue case of two-dimensional microwave billiards (Berggren et al., 2010). There is still, however, a challenge to design and implement real semiconductor devices with the above characteristics.
The physics associated with PT-symmetry is common for a number of wave phenomena and there is a rich and rapidly expanding literature. This includes, for example, electromagnetic systems, in particular in the fields of optics and photonics for which many new possibilities have opened up. Complex potentials in terms of complex refractive indices enter here in a natural way. Thus possible systems to study are co-axial waveguides, microwave billiards and more. In classical mechanics the same kind of behavior may be realized by means of a driven and a damped pendulum coupled to each other. Also in electronics when two RLC−circuits are inductively coupled, one with amplification and one with attenuation, a PT-symmetric system is obtained with EPs that can be studied in details. This shows that PT-symmetry phenomena are ubiquitous in quantum as well as electrical systems. For recent updates and reviews see (Christodoulides et al., 2017; Konotop et al., 2016; Rotter & Bird, 2015) which shows that the present field is an expanding one within fundamental science and technology. Most recently it has also been shown how the formalism for non-Hermitian quantum physics with gain and loss may be used to analyse a very different kind of system, namely photosynthesis (Eleuch & Rotter, 2017).
Finally, it is exciting to find that there is a much older field of physics with its very own traditions and literature that relates to vibrations in string instruments like violins, cellos and pianos (Gough, 1981; Weinreich, 1977, 1979). One thus talks about wolf-notes which are unfortunate facts of life for, for example, cellists who may have to struggle with and tame "wolf cellos." Wolf notes refer to unwanted interactions of different modes and how these coalesce into damped degenerate states at certain frequencies.  The similarity with EPs that appear in non-Hermitian quantum systems as described above for a quantum dot and illustrated in Figure 2 is obvious. We therefore wish to name such features “quantum wolves.”

References

Bender, C. M., & Boettcher, S. (1998). Real Spectra in Non- Hermitian Hamiltonians Having PT-Symmetry. Physical Review Letters, 80(24), 5243-5246. doi:10.1103/PhysRevLett.80.5243
Bender, C. M. (2005). Introduction to PT-Symmetric Quantum Theory, Contemporary Physics, 46, 277-292. doi:10.1080/00107500072632
Bender, C. M. (2007). Making Sense of Non-Hermitian Hamiltonians. Reports on Progress in Physics, 70, 947-1018. doi:10.1088/0034-4885/70/6/R03
Berggren, K.-F., Yakimenko. I. I., & Hakanen, J. (2010).  Modeling of open quantum dots and wave billiards using imaginary potentials for the source and the sink. New Journal of Physics, 12, 073005-19. doi:10.1088/1367-2630/12/7/073005
Christodoulides, D., El-Ganainy, R., Peschel, U., & Rotter, S. (2017). Focus on Parity-Time Symmetry in Optics and Photonics, New Journal of Physics (A series of selected articles commencing 2014).
Dembowski, C., Gräf, H.-D., Harney, H., Heine, A., Heiss, W., Rehfeld, H., & Richter, A. (2001). Experimental Observation of the Topological Structure of Exceptional Points. Physical Review Letters, 86(5), 787-790. doi:10.1103/PhysRevLett.86.787
Eleuch, H., & Rotter, I. (2017). Gain and loss in open quantum systems. Physical Review E 95, 062109-1-11, doi:10.1103/PhysRevE.95.062109.
Ferry, D. K., Goodnick, S. M., & Bird, J. P. (2009). Transport in Nanostructures. Cambridge University Press, 2nd edition.
Gao, T., Estrecho, E., Bliokh, K. Y., Liew, T. C. H., Fraser, M. D., Brodbeck, S.,… Ostrovskaya E. A. (2015). Observation of non-Hermitian degeneracies in a chaotic exciton-polariton billiard. Nature 526(7574), 554-558. doi:10.1038/nature15522
Gough, C. E. (1981). The theory of string resonances on musical instruments. Acustica 49, 124-141.
Klimov, V. I. (2010). Nanocrystal Quantum Dots. CRC Press, 2nd edition. CRC Press: ISBN 9781420079265
Konotop, V. V., Yang, J., & Zezyulin, D. A. (2016). Nonlinear waves in PT -symmetric systems. Review of Modern Physics, 88, 035002-59. doi:10.1103/RevModPhys.88.035002
Moiseyev, N. (2011). Non-Hermitian quantum mechanics. Cambridge University Press.
Rotter, I., & Bird, J. P (2015). A review of progress in the physics of open quantum systems: theory and experiment. Reports on Progress in Physics, 78, 114001-37. doi:10.1088/0034-4885/78/11/114001
Tellander, F., & Berggren, K.-F. (2017). Spectra, current flow and wave function morphology in a model PT −symmetric quantum dot with external interactions. Physical Review A, 94(4), 042115-12. doi:10.1103/PhysRevA.95.042115
Schiff, L. I. (1968). Quantum mechanics. International Series in pure and applied physics (New York) ISBN : 0070856435 or other basic textbooks on QM.
Schwarz, L., Cartarius, H., Musslimani, C. H., Main, J., & Wunner, G. (2017). Vortices in Bose-Einstein condensates with PT-symmetric gain and loss, Physical Review A, 95(5), 053613-9. doi:10.1103/PhysRevA.95.053613
Weigert, S. (2004). The physical interpretation of PT -invariant potentials, Czechoslovak Journal of Physics, 54, 1139-11142. doi:10.1023/B:CJOP.0000044016.95629.a7
Weinreich, G. (1977). Coupled piano strings. The Journal of the Acoustical Society of America, 62, 1474-84. oi:10.1121/1.381677;
Weinreich, G. (1979). The coupled motion of piano strings. Scientific American, 240, 118-127. doi:10.1038/scienticamericn0179-118